What is the product of two matrices?
What is the dot product of two matrices?
What is the multiplication of two matrices?
I studied linear algebra in collage in 1984. I wrote my first computer program in Fortran in 1982 using punch cards. I wrote my first matrix multiplication program on an Texas Instruments Calculator in 1985. I started working with numpy matrices in 2019, which is 36 computer-age-years later.
At my first attempt at numpy matrix multiplication I did not get the expected results. As I dug into the documenation, I was very confused because the use of the words “multiply” and “matrix” have different meanings between my text book from late 20th century and early 21st century numpy.
Since I have not studied mathematics formally since completing my masters in the 1990s, I will not claim the linear algebra definitions have not changed, I will only refer to the “text book” I used in the 1980s.
Here is what I learned: numpy matrix multiplication is not mathematical matrix multiplication. But the numpy dot product is what I learned as matrix multiplication back in 1984, sort of….
Text book definition
Here is my text book definition of the “product” of two matrices.

Notice the introduction to the concept at the top of the page, I quote:
Perhaps the most natural definition of matrix multiplication would seem to be: “multiply corresponding entries together.” Surprisingly, however, this definition would not be very useful for most problems.
P 26, Elementary Linear Algebra, Fourth Edition, by Howard Anton
The author explicitly says multiplying corresponding elements is not the definition of matrix multiplication, but this is precisely the numpy definition of matrix multiplication.
However, numpy does provide a mathematically correct method to compute the product of two matrices, referred to as the ‘dot’ product. To confuse matters more, in my text book, dot product refers only to vectors (1D matrices). In numpy, it refers to N-D matrices.
Definition of numpy Matrix Multiplication
For reference:
https://numpy.org/doc/stable/user/basics.broadcasting.html
https://numpy.org/doc/stable/reference/generated/numpy.multiply.html
The numpy.multiply() function simply multiplies corresponding elements. This requires that arrays have the same dimensions. If you attempt to multiply two matrices of different dimensions, numpy will either ‘broadcast’ the array to create a matching size, or throw an error if broadcasting will not work. For example:
Given ![]() and
and ![]()
What is ![]()
numpy array math is not standard mathmatics. As a python numpy developer you have to be very aware of the nuances of lists of numbers, lists of lists, numpy vectors and numpy arrays as the results you get on common operations will differ.
In this example I will only discuss the case of mumpy matrices (array with two dimensions). So, in python, using standard multiplication (* == np.multiply()):
>>> import numpy as np
>>> w = np.array([[1,5,-3,2] ]).transpose() # defined as a numpy 2-D array of 1 x 4, if we used vectors,
>>> x = np.array([ [8,2,4,7] ]).transpose() # the transpose would not work
>>> wt = w.transpose()
>>> wtx = wt * x
>>> wtx
array([[ 8, 40, -24, 16],
[ 2, 10, -6, 4],
[ 4, 20, -12, 8],
[ 7, 35, -21, 14]])Notice we get a 4 x 4 matrix as a result. Not at all what we expect from the text book definition. The text book definition of multiplying a 1 x 4 vector with a 4 x 1 vector is a 1 dimensional entity, a scalar (in the example, the result should be the value of 20).
What happened was numpy first broad cast the arrays to match dimensions:
![]() becomes:
becomes:

and,
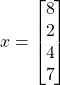 becomes:
becomes:

So simply multiplying the corresponding elements we get a 4 x 4 matrix:

Getting the Mathematically Correct Answer
To get the text book correct result, just use the numpy dot() method:
>>> wtx = wt.dot(x)
>>> wtx
array([[20]])But be aware, the correct format of the answer should be the scaler value 20, which numpy displays a 1 x 1 matrix.