Mathematical Definition of a Dot Product
The dot product of two vectors 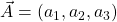 and
and 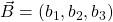 is a scaler given by:
is a scaler given by:
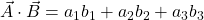
Vectors In Python/Numpy
How can we use numpy to solve generalized vector dot products such as the one below:
Given 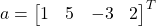 and
and 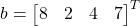
What is 
Using python and the numpy library, we have two options for expressing this calculation, 1-D arrays, and matrices. But each has a caveat to consider.
In all code examples below assume we have imported the numpy library:
>>> import numpy as np
Vector as 1-D Array
In python, using the numpy library, a vector can be represented as 1-D array or an Nx1 (or 1xN) matrix. For example:
>>> a = np.array([1,5,-3,2]) # create 1-D array, a simple list of numbers
>>> a
array([ 1, 5, -3, 2])
>>> a.shape
(4,) # shape is shown to be a 1-D array
If we take a transpose of the 1-D array, numpy will return the same dimension. So a transpose function has no effect on a numpy 1-D array.
>>> a
array([ 1, 5, -3, 2])
>>> a.shape # shape of a is 4
(4,)
>>> at = a.transpose()
>>> at.shape
(4,)
>>> at
array([ 1, 5, -3, 2]) # shape of a-transpose is also 4
>>> at.shape
(4,)
So if we define a vector ‘a’ and a vector ‘b’ and try to find the dot product of the transpose of ‘a’ to ‘b’, the transpose will have no effect, but numpy will dot product the two single dimension vectors with this result:
>>> a
array([ 1, 5, -3, 2])
>>> b
array([8, 2, 4, 7])
>>> c = np.dot(a,b) # take the dot product of 1-D vectors a and b
>>> c
20 # the result is a scalar of value 20
Note the result is the expected value of 20, and it is a scalar as expected. So when using numpy 1-D arrays for dot products, the user has to be aware that transpose functions are meaningless but also will not affect the dot product result.
Vector as a row/column of a 2-D Matrix
If we create the vector a as a numpy 2-D matrix by using the double brackets (single row, multi-column), the resulting matrix is shown below.
>>> a = np.array([ [1,5,-3,2] ]) # single row, multi-column array with dimensions 1x4
>>> a
array([[ 1, 5, -3, 2]])
>>> a.shape
(1, 4) # shape is shown to be a NxM array with N=1, M=4
If we then take the transpose of a, we get:
>>> at = a.transpose()
>>> at # the transpose of a is now a 4x1 (4 row, 1 col) matrix
array([[ 1],
[ 5],
[-3],
[ 2]])
>>> at.shape
(4, 1) # shape is shown to be a NxM array with N=4, M=1
So back to our generalized problem (defined above), what is  , using numpy matrices:
, using numpy matrices:
a = np.array([ [1,5,-3,2] ]).transpose() # implement a as given above
at = a.transpose() # get a transpose
b = np.array([ [8,2,4,7] ]).transpose() # implement b as given above
c = np.dot(at,b) # get the aT dot b
>>> c # print the contents of c
array([[20]])
We see that we can use the transpose as expected, and get the expected result of 20, but the result is expressed as a 1×1 matrix rather than the expected scaler.
Also, note, dot products of matrices are only defined as the product of matrices with orthogonal dimensions of (1xN dot Nx1), or (Nx1 dot 1xN). If you attempt to take the dot product of a Nx1 and Nx1, for example, you will get an error:
>>> c=np.dot(a,b)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<__array_function__ internals>", line 6, in dot
ValueError: shapes (1,4) and (1,4) not aligned: 4 (dim 1) != 1 (dim 0)
Conclusion
If numpy 1-D arrays are used for dot product, the user has to understand that transpose functions have no meaning. On the other hand, if numpy matrices are used, the transpose function has the expected meaning but the user has to remember to translate the 1×1 matrix result to a scaler result.






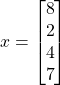 becomes:
becomes:
